Derivadas Implícita

 Derivadas Implícita

Las derivadas implícitas son un método utilizado en cálculo para encontrar la derivada de una función cuando esta no está expresada de manera explícita. 

En lugar de tener una función claramente despejada, la relación entre las variables 

x e y se da mediante una ecuación implícita en la que y no está despejada directamente en términos de x

 Es una técnica para calcular la derivada de una variable dependiente (en este caso y) con respecto a una variable independiente (en este caso x), cuando y está implícitamente definida en términos de x a través de una ecuación.

Concepto Básico

Cuando una ecuación relaciona x e y de manera implícita, por ejemplo, mediante una ecuación como:

$\mathrm{F(x,y)=0}$

y queremos encontrar dx/dy​, usamos la derivada implícita. La idea es derivar ambos lados de la ecuación respecto a x, tratando a $y$ como una función de x. Esto implica que al derivar cualquier término que incluya y, se debe usar la regla de la cadena.

Derivadas de Orden Superior

 Derivadas de Orden Superior.

Conocimiento personal.

En la clase que impartió el docente, se abordó el tema de las Derivadas de Orden Superior, donde se destacó cómo las derivaciones de una función pueden transformarse y distinguirse en múltiples formas. Inicialmente, se calcula la derivada de una función, identificada como $y'$, y el resultado de esta derivación se puede seguir derivando, identificándose como $y''$, $y'''$, así sucesivamente. Esto significa que una función puede derivarse tantas veces como sea necesario según los requisitos del problema.

Este método implica aplicar repetidamente la regla de derivación a la función original. Por ejemplo, si tenemos una función $y = f(x)$:

• La primera derivada, $y'$, representa la tasa de cambio instantáneo de $y$ respecto a $x$.
• La segunda derivada, $y''$, describe cómo cambia la pendiente de $y$ con respecto a $x$.
• La tercera derivada, $y'''$, muestra cómo varía la concavidad de la curva de $y$.
• Y así sucesivamente, con la $n$-ésima derivada, $y^{(n)}$, revelando información más detallada sobre la función original.

Este proceso es crucial en matemáticas y disciplinas como la física y la ingeniería, donde se necesita comprender la dinámica de los sistemas en términos de tasas de cambio y aceleraciones.

 La práctica regular con diversos ejemplos ayuda a fortalecer las habilidades en el cálculo de derivadas de orden superior, preparando para enfrentar problemas más complejos y situaciones del mundo real.

Dominar este concepto proporciona una base sólida para el análisis avanzado y la modelización en diferentes campos, donde las derivadas de orden superior son herramientas fundamentales para explorar fenómenos complejos y tomar decisiones informadas.

Conocimiento de consulta.

Las derivadas de orden superior son un concepto fundamental en el cálculo diferencial que permite analizar cómo cambian las tasas de cambio de una función a medida que se aplican derivaciones sucesivas. Este proceso no solo proporciona información sobre la pendiente de una función, sino también sobre cambios en la concavidad y otras propiedades importantes de la curva.

Concepto y Aplicación

Las derivadas de orden superior se obtienen aplicando la derivada a la función original repetidamente. La primera derivada $y' = \frac{dy}{dx}$ representa la tasa de cambio instantánea de $y$ respecto a $x$. La segunda derivada $y'' = \frac{d^2y}{dx^2}$ describe cómo cambia la pendiente de $y$ con respecto a $x$, revelando información sobre la concavidad de la curva.

Así, la $n$-ésima derivada $y^{(n)} = \frac{d^ny}{dx^n}$ proporciona detalles cada vez más refinados sobre la función original.

Ejemplo

Consideremos la función $y = x^3$:

1. Primera derivada: $y' = \frac{d}{dx}[x^3] = 3x^2$
   

2. Segunda derivada: $y'' = \frac{d}{dx}[3x^2] = 6x$
   

3. Tercera derivada: $y^{\mathrm{\prime }\mathrm{\prime }\mathrm{\prime }}=\frac{d}{dx}[6x]=6$

4. Cuarta derivada: $y^{(4)} = \frac{d}{dx}[6] = 0$
   

En este ejemplo, vemos cómo cada derivada sucesiva nos da información adicional sobre la función original $y = x^3$, desde la pendiente inicial hasta detalles sobre la curvatura y la aceleración.

Importancia y Aplicaciones

Las derivadas de orden superior son esenciales en disciplinas como la física, la economía y la ingeniería, donde se utilizan para modelar fenómenos complejos y tomar decisiones informadas. Estas herramientas matemáticas permiten entender mejor el comportamiento de sistemas dinámicos y optimizar procesos en diversas aplicaciones prácticas.

Validación y Referencias

Para validar esta información, autores reconocidos en el campo del cálculo diferencial y las matemáticas incluyen:

• Michael Spivak en "Cálculo Infinitesimal".

• James Stewart en "Cálculo de Varias Variables".

• Tom M. Apostol en "Cálculo".

• Ron Larson en "Cálculo y Geometría Analítica".

Estos autores proporcionan una base teórica sólida y ejemplos aplicados que respaldan la comprensión de las derivadas de orden superior y su importancia en el análisis matemático.

Conclusión

Dominar las derivadas de orden superior es crucial para profundizar en el análisis matemático y modelar problemas del mundo real. La práctica con ejemplos variados y la comprensión de las propiedades derivativas permiten a los estudiantes y profesionales aplicar estas herramientas con confianza en diversos contextos académicos y profesionales.

Derivadas exponenciales y logarítmicas

Derivadas exponenciales y logarítmicas

Conocimiento personal.

En la clase de cálculo diferencial, el maestro nos sorprende con un conocimiento sobrenatural al presentarnos las últimas reglas que utilizaremos a lo largo de este camino de crecimiento y conocimiento. Le agradezco sin más preámbulos y comenzamos con el nombre de Euler, que es una constante matemática aproximadamente igual a 2.71828, y la otra es LN, que significa logaritmo natural. Al principio, empezamos con procedimientos sencillos, pero al avanzar, me perdí en el desarrollo de las operaciones. En las funciones que debíamos derivar, se requería aplicar una combinación de reglas complicadas y ahí es donde tuve dificultades. Personalmente, considero que no tengo esa capacidad innata para resolver los problemas que se plantearon en clase. Sin embargo, gracias a vídeos y a la investigación, he logrado entender y practicar la solución de las funciones.

Conocimiento de consulta.

Euler y la Constante e:

Leonhard Euler, un matemático suizo del siglo XVIII, es conocido por sus numerosas contribuciones al campo de las matemáticas, entre ellas la introducción de la constante matemática e. La constante e se define como el límite de (1 + 1/n)^n cuando n tiende a infinito, y tiene un valor aproximado de 2.71828. Euler demostró que e es fundamental en el cálculo diferencial e integral, ya que aparece naturalmente en muchas situaciones donde el crecimiento exponencial está presente.

Citas y referencias:

• Euler, L. (1748). Introductio in analysin infinitorum. En esta obra, Euler desarrolla el concepto de la constante e y su importancia en el cálculo diferencial.

• Stewart, J. (2011). Cálculo de una variable: Trascendentes tempranas. Editorial Cengage Learning. Stewart explica cómo la constante e emerge en el contexto del crecimiento exponencial y su derivación en el cálculo diferencial.

Logaritmo Natural (LN):

El logaritmo natural, denotado como LN o ln(x), es el logaritmo en base e. Es fundamental en cálculo diferencial porque la derivada del logaritmo natural de una función es esencial para calcular tasas de cambio relativas. Se define como la integral indefinida de 1/x, lo que significa que ln(x) representa el área bajo la curva 1/t desde t=1 hasta t=x. El logaritmo natural tiene aplicaciones en áreas como la física, la economía y la biología, donde las tasas de crecimiento y decaimiento se modelan usando esta función.

Citas y referencias:

• Simmons, G. F. (2007). Cálculo con geometría analítica. McGraw-Hill. Simmons aborda el logaritmo natural como parte integral del estudio del cálculo diferencial, explicando su definición, propiedades y aplicaciones.

• Spivak, M. (1967). Cálculo Infinitesimal. Publicación independiente. Spivak explora profundamente las bases del cálculo diferencial, incluyendo el tratamiento del logaritmo natural y su relación con la derivación.

Euler y el logaritmo natural (LN) tienen aplicaciones importantes en la vida cotidiana, desde situaciones financieras hasta ciencias naturales. Aquí te presento algunas áreas donde se utilizan estas constantes y funciones:

1. Intereses Compuestos en Finanzas: En el ámbito financiero, la constante matemática e de Euler se utiliza para calcular intereses compuestos. Por ejemplo, cuando se calculan los intereses sobre una inversión que se capitaliza continuamente, la fórmula utiliza e como base exponencial. Esto es crucial en la planificación financiera y en la evaluación de inversiones a largo plazo.

2. Modelado de Crecimiento y Decaimiento: El logaritmo natural (LN) se usa ampliamente para modelar fenómenos de crecimiento y decaimiento en biología, química, física y economía. Por ejemplo, en biología, las poblaciones que crecen o disminuyen exponencialmente se modelan con funciones que involucran el logaritmo natural. En economía, el crecimiento económico o el decaimiento de ciertas variables económicas pueden ser modelados usando LN.

3. Probabilidad y Estadística: En el campo de la probabilidad y la estadística, LN se utiliza en la distribución normal y en otros modelos estadísticos. La distribución normal está relacionada con la función exponencial que usa e como su base, lo que la hace fundamental para comprender y analizar datos en diversos contextos, desde la investigación científica hasta la toma de decisiones empresariales.

4. Ingeniería y Tecnología: En ingeniería y tecnología, tanto Euler como LN son esenciales para diseñar algoritmos eficientes, modelar sistemas dinámicos y simular comportamientos complejos. Por ejemplo, en el diseño de circuitos eléctricos, el análisis de sistemas de control o la programación de computadoras, estas herramientas matemáticas son utilizadas para resolver problemas y optimizar soluciones.

5. Medicina y Ciencias de la Salud: En medicina, el logaritmo natural se utiliza para modelar la cinética de los fármacos en el cuerpo humano y para comprender el crecimiento y la regresión de enfermedades. Además, las aplicaciones de e y LN son fundamentales en estudios epidemiológicos y en la investigación de enfermedades, donde la modelización matemática ayuda a prever la propagación de enfermedades y a diseñar estrategias de prevención.

Estos son solo algunos ejemplos de cómo Euler y el logaritmo natural se aplican en situaciones cotidianas. Su utilidad va más allá del aula de matemáticas, afectando muchos aspectos de nuestras vidas y la comprensión del mundo que nos rodea.

Reglas de derivación algebraicas y trigonométricas

 
 Derivación algebraicas y trigonométricas.

Conocimiento personal.

En el contexto del cálculo diferencial, las reglas de derivación trigonométrica desempeñan un papel fundamental al permitirnos encontrar la tasa de cambio instantánea de funcione
s que incluyen términos trigonométricos como el seno, coseno, tangente, entre otros. Estas reglas son enseñadas detalladamente en un anexo presentado por el docente durante nuestras clases. Este anexo explora cinco reglas principales, cada una ilustrada con tres ejemplos para facilitar la comprensión y aplicación práctica de las mismas.

Importancia y Aplicación

Las funciones trigonométricas son omnipresentes en problemas que involucran fenómenos periódicos y oscilatorios, comunes en física, ingeniería y ciencias naturales. Dominar las reglas de derivación trigonométrica no solo mejora nuestra capacidad para resolver problemas teóricos, sino que también nos equipa para abordar situaciones prácticas donde estas funciones son cruciales para modelar y predecir comportamientos complejos.

Conocimiento de consulta.

La derivación de las funciones trigonométricas

 es el proceso matemático de encontrar el ritmo al cual una función trigonometrica cambia respecto de la variable independiente; es decir, la derivada de la función. Las funciones trigonométricas más habituales son las funciones sen(x), cos(x) y tan(x). Por ejemplo, al derivar f(x) = sen(x), se está calculando la función f'(x) tal que da el ritmo de cambio del sen(x) en cada punto x.

Regla de la cadena

La regla de la cadena es una fórmula para calcular la derivada de la composicion de dos o más funciones. Esto es, si f y g son dos funciones, entonces la regla de la cadena expresa la derivada de la funcion compuesta f ∘ g en términos de las derivadas de f y g. Por ejemplo , la regla de la cadena de f ∘ g (x) ≡ f [g (x)] es

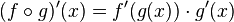
o escrito en notación de Leibniz

Ejemplo:

f(x)=(2x³+3)³

f ‘(x)=3(2x³+3)²(6x²)

f ‘(x)=18x²(2x³+3)²

Derivada de un cociente

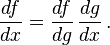
La derivada de un cociente se determina por la siguiente relación:

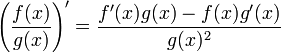
Para aquellos que se puedan confundir por algunas variables de más se puede escribir así:

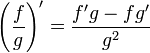
Es decir:

«La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado».

Este caso se relaciona mucho con la regla de derivada de un producto, pero hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando lo dicho anteriormente consideremos como ejemplo la siguiente función:

Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es  y se multiplique por la derivada del numerador que seria 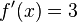; luego la segunda parte dice que tomemos la función del numerador () sin derivar y lo multipliquemos por la derivada de , que seria 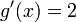, todo esto lo dividimos entre el denominador al cuadrado, así:

Ahora todo es cuestión de simplificar:

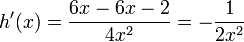
Cálculo Diferencial e Integral" por William Anthony Granville.

Análisis Matemático I: Cálculo Diferencial" por Eduardo Espinoza Ramos.