Derivación algebraicas y trigonométricas.
Conocimiento personal.
En el contexto del cálculo diferencial, las reglas de derivación trigonométrica desempeñan un papel fundamental al permitirnos encontrar la tasa de cambio instantánea de funcione
s que incluyen términos trigonométricos como el seno, coseno, tangente, entre otros. Estas reglas son enseñadas detalladamente en un anexo presentado por el docente durante nuestras clases. Este anexo explora cinco reglas principales, cada una ilustrada con tres ejemplos para facilitar la comprensión y aplicación práctica de las mismas.
Importancia y Aplicación
Las funciones trigonométricas son omnipresentes en problemas que involucran fenómenos periódicos y oscilatorios, comunes en física, ingeniería y ciencias naturales. Dominar las reglas de derivación trigonométrica no solo mejora nuestra capacidad para resolver problemas teóricos, sino que también nos equipa para abordar situaciones prácticas donde estas funciones son cruciales para modelar y predecir comportamientos complejos.
Conocimiento de consulta.
es el proceso matemático de encontrar el ritmo al cual una función trigonometrica cambia respecto de la variable independiente; es decir, la derivada de la función. Las funciones trigonométricas más habituales son las funciones sen(x), cos(x) y tan(x). Por ejemplo, al derivar f(x) = sen(x), se está calculando la función f'(x) tal que da el ritmo de cambio del sen(x) en cada punto x.
Regla de la cadena
La regla de la cadena es una fórmula para calcular la derivada de la composicion de dos o más funciones. Esto es, si f y g son dos funciones, entonces la regla de la cadena expresa la derivada de la funcion compuesta f ∘ g en términos de las derivadas de f y g. Por ejemplo , la regla de la cadena de f ∘ g (x) ≡ f [g (x)] es
o escrito en notación de Leibniz
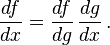
- Ejemplo:f(x)=(2x³+3)³f ‘(x)=3(2x³+3)²(6x²)f ‘(x)=18x²(2x³+3)²
Derivada de un cociente
La derivada de un cociente se determina por la siguiente relación:
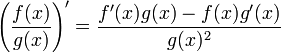
Para aquellos que se puedan confundir por algunas variables de más se puede escribir así:
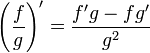
Es decir:
«La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado».
Este caso se relaciona mucho con la regla de derivada de un producto, pero hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando lo dicho anteriormente consideremos como ejemplo la siguiente función:

Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es  y se multiplique por la derivada del numerador que seria
y se multiplique por la derivada del numerador que seria 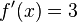 ; luego la segunda parte dice que tomemos la función del numerador (
; luego la segunda parte dice que tomemos la función del numerador ( ) sin derivar y lo multipliquemos por la derivada de
) sin derivar y lo multipliquemos por la derivada de  , que seria
, que seria 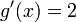 , todo esto lo dividimos entre el denominador al cuadrado, así:
, todo esto lo dividimos entre el denominador al cuadrado, así:

Ahora todo es cuestión de simplificar:
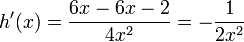
Cálculo Diferencial e Integral" por William Anthony Granville.
Análisis Matemático I: Cálculo Diferencial" por Eduardo Espinoza Ramos.


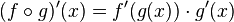

.jpeg)


No hay comentarios.:
Publicar un comentario